濾材の濾過能力はその形で決まるが、どの形が能力にどう関係するのかが不明だった。専門メーカーの話からその方法がわかったので、各種濾材の能力を計算で求めてみた。
濾材の性能を左右する要素
1999/7/30 の下水道展において、濾材を作る専門メーカーの方から、濾材の見た目から能力を知るためのヒントを得た[1]。内容を以下に再掲する。
1.生物濾過の能力は、水との接触面積によって決まる。
2.長期的な有効接触面積は、1mm以下の細かい凹凸を無視した表面積に等しくなる(多孔質の微細構造は、発生するバクテリアですぐに詰まってしまいろ過面積に寄与しない)。
3.生物濾過膜の表層から5ミクロンより深い部分は、酸素が届かないため生物濾過は機能しない。
4.多孔質の濾材はバクテリアの定着が早い。
5.濾材の形状は「くら型」がもっともよい。
(2)(3)は、濾過能力は表面だけで決まり、水の通りが悪い内部の多孔質構造や、濾材の材質は関係しないことを意味している。例えば「1gの活性炭の表面積はテニスコート4面分にもなる」という話は空気中に置いた場合であって、水中の濾過面積は見た面の表面積だけと考えるのが正しい。
(2)は、濾過能力が時間と共に変化することを示している。つまり、ろ過能力は最初からずっと一定ではなくて、「初期性能」と「長期性能」に分けて考える必要がある。
(4)は、表現がツルツルよりザラザラしていた方が、バクテリアが取り付きやすく剥がれにくいことを意味する。このことは直感的にも理解できる。
以上のことからすると、濾材の形状を観察すれば濾過能力の推定ができそうだ。そこで、各種濾材につて濾過力を定量的に求めてみた。
濾過の初期性能と長期性能は何によって決まるか
バクテリアはどろっとした粘質のような形態になるため、ミクロンオーダの微細な構造は濾過面積に寄与しないと考えることができる。推定困難なこのミクロの凹凸が無関係になったことで、濾過面積の推定が容易になった。
これまでの観察結果から、濾過面積として有効に機能するのは、コンマ数ミリオーダの凹凸から、と考えられる。このサイズ凹凸が濾過面積として機能する期間を「初期」とし、この凹凸含めた濾材の総面積を、「初期性能」とした。初期性能の高いものは、濾過の立ち上がりも早いことが予測できる。
初期に役立ったコンマ数ミリオーダの凹凸は、その後のバクテリアの増殖とともに粘質の中に埋まってしまい、役立たなくなる。結局最後まで濾過に寄与するのは、1ミリ以下の凹凸を無視した形状の表面積だけになる。このときの表面積を、「長期性能」とした。
しかし、現実にはコンマ数ミリオーダの凹凸が全て完全に詰まるわけではないので、上記の長期性能の評価は厳しすぎるといえる。そこで、詰まり率というパラメータを導入し、初期性能で求めた表面積×詰まり率と、1ミリ以下の凹凸を無視した前記表面積との、いずれか大きい方を長期性能と定めることにした。
各種濾材の観察
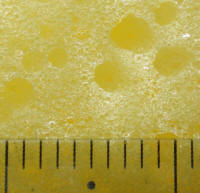
濾材を詳しく観察するため、拡大写真を撮影した。
左から大磯砂(細目)、ウールマット、洗車スポンジ(洗車スポンジ濾材)、シポラックス。写真に写っているスケールの1目盛りは1mm 。微細構造のサイズはなんとか目視で確認できる。このほかにも空隙率や単位体積当たりの濾材個数を測定した。これらの結果をまとめたものが次の表だ。
表1.各種濾材の形状観察結果
| 種類 | 微細構造のサイズ | 空隙率(%) | 単位体積あたりの個数(個/L) |
| 大磯(細目) | 10ミクロン以下 | 0 | 1.12×105 |
| ウールマット | 0.2~0.4mm | 98.4 | 1 |
| 洗車スポンジ濾材(小) | 0.3mm前後 | 98.4 | 1725 |
| 洗車スポンジ濾材(中) | 0.3mm前後 | 98.4 | 480 |
| シポラックス | 0.3mm前後 | 67.1 | 200 |
微細構造のサイズとは、濾材の基本的な多孔質構造を形成している気泡のサイズや、繊維間隔のことであり、写真に写っているスケールと比較することで概略のサイズを求めることが出来る。
大磯を除くと大体0.3mm前後で共通してるようだ。ウールマットを構成するナイロン繊維の太さは、正確にはわからなかったが、今回は0.01mmとした。
大磯は粒の表面積だけが濾過に寄与するので、外形寸法を知るのが重要になる。細目大磯は写真のようにいろんなサイズの粒が混じっているが、これらの体積が、球または立方体で表すと平均していくつになるかがわかればよい。今回は1辺が1.6mmの立方体と仮定した。
空隙率とは多孔質構造内部に存在する空隙部の割合を表し、これは濾材の比重を実測して材料そのものの比重との比から求めた。ウールマットと洗車スポンジの空隙率は偶然にもほぼ同じである。
 単位堆積あたりの個数は、1リットルにその濾材が何個入るかを示す。これは最終的に濾過容器に濾材を詰めたときの濾過能力を計算するために重要なパラメータだ。
単位堆積あたりの個数は、1リットルにその濾材が何個入るかを示す。これは最終的に濾過容器に濾材を詰めたときの濾過能力を計算するために重要なパラメータだ。
一般に、濾材は複数を容器に入れて使うため、容器に入れたときの体積あたりの面積で評価しなければなならい。このパラメータは、濾材の粒に比べ十分大きな容器に定量入れ、入った個数に1個あたりの表面積を乗じることで計算出来る。左の写真は、シポラックスを300cc入れて測定している様子。
多孔質構造のモデル化
濾材の初期性能を予測するには微細構造の表面積を求める必要がある。しかし、これを計算する際には、多孔質構造をどのようにモデル化するかが問題になる。モデルを検討する上で大切なことは、モデルができるだけ単純で、計算に使うパラメータが誰でも容易に入手できるものを用いた。
ウールマットは繊維の集まりであるから、繊維の表面積を求め、シポラックスはトンネル構造とみなし、トンネル内壁の表面積で評価することにした。
 問題は洗車スポンジ濾材である。この原料となっている洗車スポンジは気泡の集まりというよりは左の写真のように骨格だけの構造物に近い。これに所々隔壁が存在する。
問題は洗車スポンジ濾材である。この原料となっている洗車スポンジは気泡の集まりというよりは左の写真のように骨格だけの構造物に近い。これに所々隔壁が存在する。
ちなみに左の写真は洗車スポンジよりずっと気泡の大きな別のスポンジを撮影したもので、隔壁はまったくない。洗車スポンジに光を当てるとキラキラ光る部分があるが、これが隔壁。
そこで骨格構造、気泡構造、トンネル構造などのモデルを考え、実際に試算した結果、トンネル構造として扱うのがもっとも実体に近いと判断した※。
トンネル構造モデルによる表面積は、トンネルの直径=微細構造のサイズ、トンネルの体積=濾材の空隙率(空隙の体積)とおくことで、容易に求めることが出来る。
サブストラットは多孔質構造と言うよりはガラスの粉末を何らかのツナギを使って固めたものであり、トンネル構造モデルは適用できない。外形も不定形で表面積の計算も悩ましい部分がある。これについては今後の検討課題である。
※骨格構造では隔壁が考慮されないため結果が小さすぎ、また気泡構造では実際に計算で求められる数の気泡が濾材の体積の中に収まりきれないという幾何学的矛盾を生じることがわかった。
詰まり率の推定
詰まり率とは、濾材を長期間使用したときに、バクテリアによって多孔質構造が目詰まりすることで失われる、濾過面積の比率のことで、長期性能を予測する重要なパラメータである。
しかしながら、詰まり率は、微細構造のサイズのほか、気泡の独立度、空隙率、濾材自身の外径サイズなど様々な要素が絡んでおり、定式的に予測することが出来ず、現在のところ経験をもとに目算するしかない。今回の計算では、これを次のように仮定した。
表2.濾材の詰まり率(推定)
| 種類 | 詰まり率(%) |
| 大磯(細目) | 60 |
| ウールマット | 98 |
| 洗車スポンジ濾材(小) | 60 |
| 洗車スポンジ濾材(中) | 60 |
| シポラックス | 90 |
大磯の詰まり率とは粒同士の隙間の詰まり率を示している。これは濾過容器に入れる深さによって大きく左右されるため一概に言えない。大磯の詰まり率は20~30mmの深さで底面濾過をした場合の経験値だ。
ウールマットはマット状の形状が災いして古い濾過膜が外に出ていきにくいため、経験上ほとんど詰まってしまうことがわかっている。
洗車スポンジ濾材はもともと隙間だらけの骨格構造をもち、さらに大きい気泡が混ざった詰まりにくい構造になっている。シポラックスの微細構造は空隙率が低く、空隙同士の連通もよくないため、長期的にはすべて詰ってしまうと予測される。
計算結果
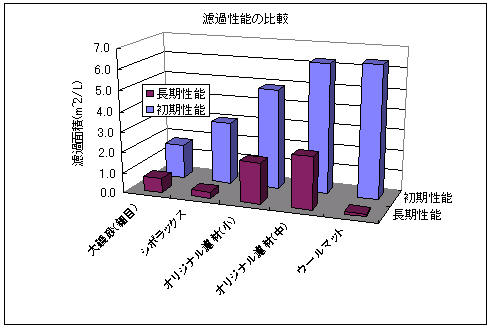
以上の前提条件をもとに計算した濾過能力(濾過面積)を以下に示す。
意外だったのは洗車スポンジ濾材の小サイズよりも中サイズの方が初期性能が高いこと。普通はサイズを減らすと表面積は2乗で減るが、体積は3乗で減るため、入る個数が増えて結果的に表面積が増えるはずだが、空隙が増えることで相殺されてしまうようだ。
この計算はいろんな前提条件や仮定条件のもとに成り立っており、これらのさじ加減でグラフは上下する。前提条件や計算式をいろいろ変えてみたい人はいると思う。計算シートを公開するのでご自分でパラメータを変えて試してみて欲しい。
<関連商品>
濾材一覧 価格の高いものが優れた濾材とは限りません
<計算ワークシート>
濾過面積計算
<関連記事>
1.洗車スポンジ濾材~発見と検証の経緯