ホイールを軽くすると、燃費が良くなる、加速が良くなる、ブレーキがよく効く、ハンドルの応答が良くなる、乗り心地が良くなる、などと言われている。しかしどれも定性的で、どの程度良くなるのか数字で示された資料が無い。そこで、これらの効果を計算してみた。
ホイールを軽くすると乗り心地はどうなるか
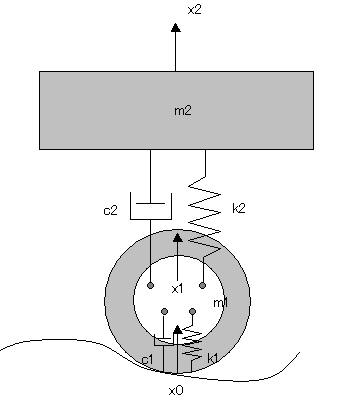
ホイールの重さを検討するためには、地面とホイールの間にばね要素(タイヤ)を考慮する必要がある。その場合の車体の振動モデルは2質点モデルとなって図1のようになる。
モデルの要素は、m1:ホイールの質量(実際にはばね下の総質量)、m2:車体の質量、k1:タイヤのばね定数、k2:サスのばね定数、c1:タイヤの減衰係数、c2:ダンパーの減衰係数、x0:路面の上下変位、x1:タイヤの上下変位、x2:車体の上下変位である。
図1のモデルの運動方程式は、次の式で表せる。
m1d2x1/dt2 + (c1 + c2)dx1/dt + (k1 + k2)x1 – c2dx2/dt – k2x2 = c1dx0/dt + k1x0 (1-1)
m2d2x2/dt2 + c2dx2/dt + k2x2 – c2dx1/dt – k2x1 = 0 (1-2)
このモデルを使って振動伝達率を求めてみよう。
これは一旦ラプラス変換して処理すると簡単だ。式(1-1),(1-2)のすべての初期値を0としてラプラス変換すると次式を得る。
X1(s)(m1s2 + c1s + c2s + k1 + k2) - X2(s)(c2s + k2) = x0(s)(c1s + k1) (1-3)
X2(s)(m2s2 + c2s + k2) - X1(s)(c2s + k2) = 0 (1-4)
sはラプラス演算子だ。
(1-3),(1-4)の式から振動伝達関数 G01 ( = X1(s)/X0(s) )、G02 ( = X2(s)/X0(s) ) を求めると、それぞれ次のようになる。
G01 = (c1s + k1)/(α – γ2/β) (1-5)
G02 = (c1s + k1)/(αβ/γ – γ) (1-6)
α = m1s2 + c1s + c2s + k1 + k2 、 β = m2s2 + c2s + k2 、 γ = c2s + k2
ここまでの解は、教科書によってはそのまま載っているものもあるだろう。
次に周波数応答を求めてみよう。s=jωとおいて、減衰がないときの振幅比(振動伝達率)の周波数応答を求めた結果を次に示す。
τ01 = | k1/(α’ – k22/β’) | (1-7)
τ02 = | k1/(α’β’/k2 – k2) | (1-8)
α’ = k1 + k2 – m1ω2 、 β’ = k2 – m2ω2
τ02が地面から車体までの振動伝達率(変位)になる。振幅x0の衝撃的な変位がタイヤに入力された場合の車体に伝わる衝撃力(加速度)はτ02を使って次式で求められる。
a02 = x0・τ02・ω2 (1-9)
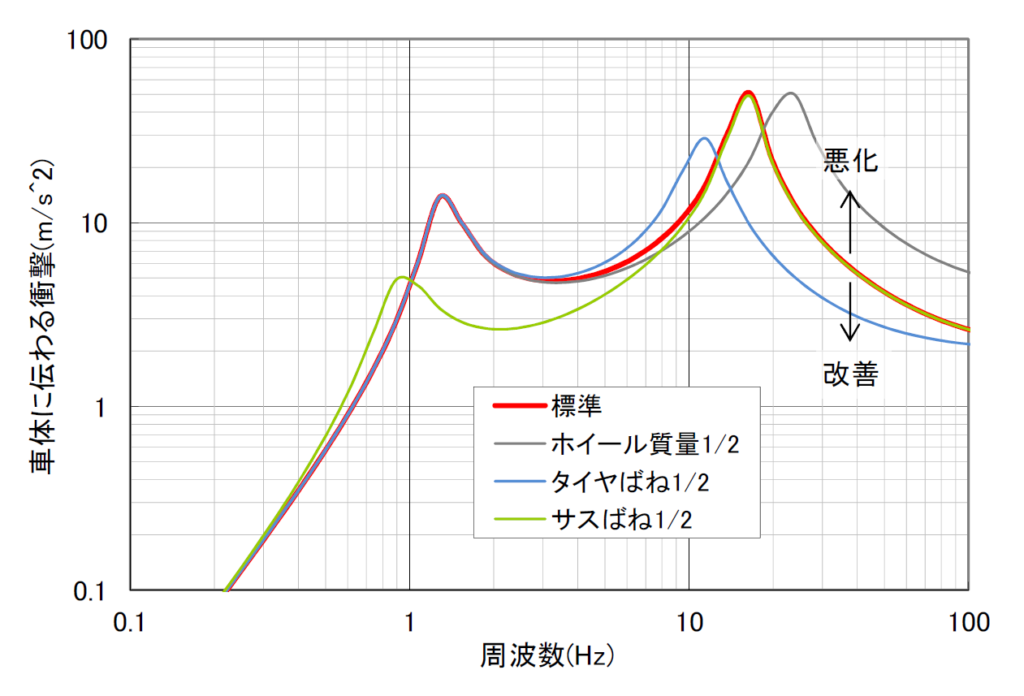
m1=20kg、 m2=300kg、 k1=2×105N/m、 k2=2×104N/m、c1=600Nm/sec(ζ=0.12)、c2=400Nm/sec(ζ=0.10)を「標準」の計算条件とし、各パラメータを標準から1/2振ったときの a02 の計算結果を次に示す。
詳細:変位入力としてx0=50mmを与えた。k1,k2は実測値を参考にしている。減衰付きの周波数応答を手計算するのはかなりしんどいので、連成を無視して1自由度の式を直結して求めた(2つのピークが離れているので、一自由度系で解いてもほぼ同じ結果を得る)。
グラフには2つのピークの山が見える。これが共振点だ。この共振点の周波数(共振周波数)は、1.2Hzと、16Hz。
防振効果は、共振周波数より高い周波数で得られる。共振周波数より下の周波数では、ばね上とばね下が一体となって動く。つまり、防振効果は得られない。
上記の標準の計算条件から、1.2Hzは車体とスプリング、16Hzはタイヤとホイールで決まる共振である。
ところで、10Hz以下の低周波は車体の上下の揺れに関係し、10Hz以上の高周波は主に突き上げの強さに関係すると考えられる。このことから、車体とスプリングは車体上下の揺れ、タイヤ&ホイールは突き上げの防振を担っていることがわかる。
以上の結果から、次の結論を得る。
- ホイールを軽くすると突き上げが増えて乗り心地が悪くなる。具体的には、ばね下質量を1/2にすると衝撃が約3倍に増える。
- タイヤのばねを減らす(扁平率をあげる)と突き上げが改善する。
- 車体上下の揺れは、タイヤやホイールを変えても改善されない。
- 車体上下の揺れは、車体を重くするか、サスペンションのばねレートを下げる(ばねを柔らかくする)ことでしか改善できない。
補足(2019/9/30)
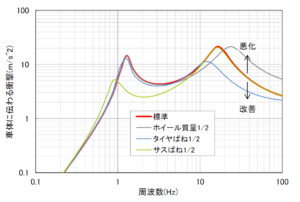
図1のような2質点系モデルの減衰を考慮した正確な振幅比は以下で計算できる。まず、式1-6を、次の形にする。
G02 = γ(c1s+k1)/(αβ-γ2) (1-10)
これを複素数の形で表す。
G02 = (je+f)(jp+q)/((ja+b)(jc+d)-(je+f)2) (1-11)
分母がこのままでは振幅を計算できないので、分母を展開して実部と虚部にまとめる。
G02 = (je+f)(jp+q)/j(ad+bc-2ef)2+(bd+e2-f2-ac) (1-13)
振幅比は次式で求められる。
τ02’=√((e2+f2)(p2+q2)/((as+bc-2ef)2+(db+e2-f2-ac)2)) (1-14)
a=ω(c1+c2)、b=k1+k2-m1ω2、c=c2ω、d=k2-m2ω2、e=c2ω、f=k2、p=c1ω、q=k1
式1-14を使って図2と同じ条件を計算した結果は次の通り。こちらの方が減衰の影響を詳しく観察できる。
ホイールを軽くするとバタバタする、跳ねやすくなるのはなぜか
ホイールを軽量化した人が「足回りがバタバタする」「飛び跳ねやすくなった」といった症状を経験することがあるようだ。
図1のモデルを見てわかるように、タイヤ&ホイールの部分は質量m1、ばね定数k1、減衰項c1、の3要素から成り、m1,k1,c1の3つのバランスから成っている。そこへ、ホイールm1だけ極端に軽くしてしまうと、c1,k1が相対的に高くなり、振動伝達率や減衰特性が悪化してバタバタしたり跳ねやすくなる。
この弊害を避けるためには、ホイール軽量化と同じ比率でタイヤの減衰率とばね定数(扁平率)もあげなければならない※1。同じことがサスペンションについてもいえる。
以上の結果から、ホイールの軽量化やローダウンでサスがバタバタする場合は、足回りの質量、減衰、ばねレートのバランスを崩した結果と考えられる。
※1:c=2ζsqrt(m・k)だから、mとkを同時に1/2にした場合、cはsqrt(0.5×0.5)=1/2にすれば元の特性を損うことがない。
インチアップorダウンで乗り心地を犠牲にしないためには
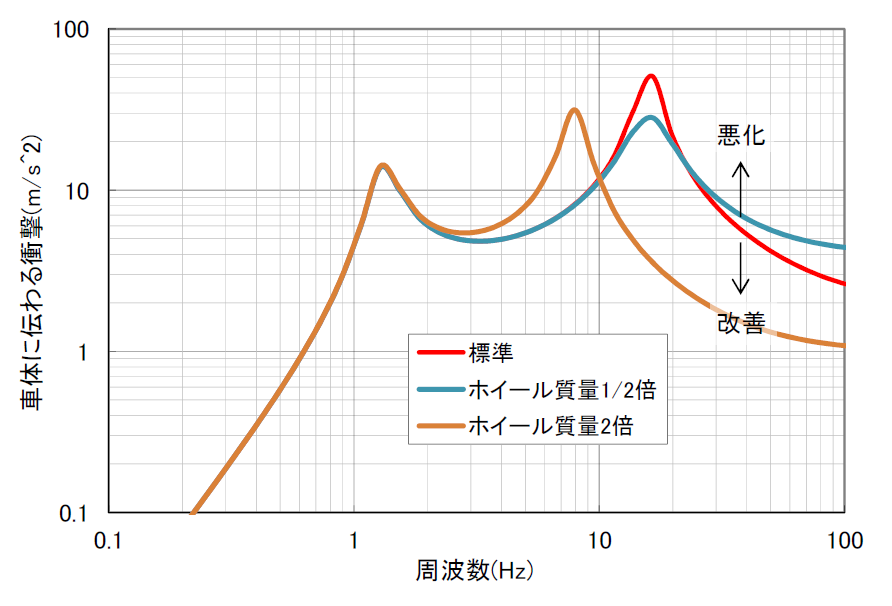
インチダウンによる乗り心地の改善を考えた場合、ホイールは軽量化or重量化、どちらが良いのだろう。グラフ1-1の標準から、インチダウンを仮定してタイヤのばね定数を1/2とし、同時にホイールの質量を2倍、1/2倍した場合の計算結果を次に示す。
インチダウンしたとき軽いホイールを選ぶと効果が相殺してしまうことがわかる。
ばね下の質量はホイールだけで決まらないので注意が要る。例えば、軽自動車など、もともとばね下の機構が単純(ばね下が軽い)なケースではホイール質量が影響しやすいが、ばね下に複雑なリンクや大型ブレーキなどが付く(ばね下が重い)ケースでは、ばね下全体の質量に占めるホイールの比率が小さいため、ホイールを軽量化しても全体としてあまり変わらない。
結局、インチダウンによって乗り心地を改善したい場合は、ホイールが軽くなり過ぎないよう注意を払い、
インチアップで少しでも乗り心地の悪化を押さえたい場合は、ホイールを現状より重くするのが正解。
「ドレスアップ」と称してローダウン&インチアップする人が多いが、このとき現状より重くなるのを嫌って軽量ホイールを選択するのは間違いだ。
それと、ローダウンやインチアップの際、ホイールの質量やタイヤの扁平率(ばね定数)を極端に変えないよう注意したい。これらがノーマルから2倍以上変わると回転軸系の曲げ、ねじりの共振点が常用域に入り、特定の速度で振動が発生して改善できなくなる恐れがある。
軽量ホイールは加速や燃費にどの程度寄与するか
ホイールを軽量化した場合、加速や燃費はどの程度良くなるのだろうか。下の表は、φ640のタイヤを履いて、0-100km/hを10秒で加速した場合の、ホイールの回転慣性による損失トルクを計算した結果だ。
表1 ホイールサイズと損失トルクの関係
| ホイールサイズ (インチ) |
リム幅 (インチ) |
リム平均肉厚 (mm) |
リム質量 (kg) |
慣性モーメント I1(kgm^2) |
損失トルク T1(Nm) |
| 17(軽量) | 7.5 | 7 | 4.82 | 0.218 | 1.89 |
| 17 | 7.5 | 10 | 6.84 | 0.304 | 2.64 |
| 16 | 7.0 | 10 | 6.00 | 0.236 | 2.05 |
| 15 | 6.5 | 10 | 5.21 | 0.180 | 1.56 |
| 14 | 6.0 | 10 | 4.48 | 0.134 | 1.16 |
表の損失トルクT1(Nm)は次式で計算できる。
T1 = I1・dω/dt (4-1)
I1:回転慣性モーメント(kgm2)、v:車速(m/s)、D:タイヤ径(m)、t:加速時間(s) 、dω/dt:ホイールの回転角加速度=2v/(D・t)(rad/s2)。この例では dω/dt=2×27.8/(0.64×10)=8.68rad/s2である。
表の一番上は17インチのホイールで軽量化を図ったもの。2番目のノーマルと比較するとリム質量は2.0kg減(4本で8.1kg)、損失トルクの差分は0.75Nm減(4本で3.0Nm)となっている。
この3.0Nmという値は、ギアの減速比を考慮すると1Nm以下。エンジントルク(排気量2Lエンジンなら通常200Nmくらい)と比較しても2桁以上小さい。従って、ホイールの回転慣性をいくら小さくしても、加速の違いを体感できる人は、まずいない。数字に表れるような燃費の向上も、全く期待出来ないと考えていい。
今度は、ホイールの進行方向の慣性に注目してみよう。この場合、ホイールの全質量が影響し、ばね下、ばね上は関係しない。進行方向の慣性による損失トルクT2は、
T2 = m・a・D/2 (4-2)
である。aは車両加速度(m/s2)で、a=v/t=100km/h/10sec=2.8m/s2。
ここで例えばホイール4本で20kg軽量化した場合、タイヤ径D=φ640とすると T2=20×2.8×0.64/2=17.8Nm を得る。つまり、ホイールの進行方向の慣性の影響は、回転慣性よりもひと桁大きいことがわかる。
以上の結果から、加速性に関しては、リムの回転慣性はほとんど影響せず、ホイールを軽くした分が単純に車体全体の質量から減算される※3と考えて良い。その効果(%)は、100×軽量化した質量(kg)/車重(kg) だけの簡単な式で定量的に見積もることが可能だ。
元々のホイールが16インチ以下の場合は、超軽量ホイールに変えてもトータルとして大幅な軽量化が出来ないため※4、高価な鍛造ホイールを使うメリットはほとんど無い。それでもなお加速感がアップしたと感じた場合は、他の変化要因(空気圧や、ころがり抵抗の変化)によるものだろう。
※3:100kgの重量増による0-100km/h 10sec加速の損失は、W=mv2/s=7.72kW=10.5馬力であるから、ほぼ車重10kgあたり1馬力損すると考えてよい。タイムに換算すると、1.4トンのクルマを100kg軽量化することで0.7秒の短縮になる。
※4:16インチのホイールは鋳造品でも9kg前後の物が多い。これをたとえ半分に軽量化できたとしても4本合わせて18kgの軽量化にしかならない。
ホイールを軽くするとステアリングも軽くなるか
回転しているホイールの切り角を変えると、その軸回りの回転慣性によるトルク反力T3(Nm)と、ジャイロモーメントJm(Nm)の2つがホイールに作用する。これらは、それぞれ次式で示される。
T3 = I2・dωs/dt (5-1)
Jm = I1・ωn・ωs (5-2)
I2:ホイール切り角に関する回転慣性(Kgm2):dωs/dt :ホイール切り角の角加速度(rad/s2)、I1:ホイール回転慣性モーメント(Kgm2)、ωn:ホイールの回転速度(rad/s)、ωs :ホイール切り角の角速度(rad/s)
表4-1の17インチホイールを軽量化した例で考えると、I2は、前輪2本で0.10Kgm2 の低減※5。回転慣性I1は2本で0.17Kgm2 の低減になる。
※5: 17インチホイールのl2 = 0.17Kgm2、17インチ軽量のl2 = 0.12Kgm2 (ホイール1本あたり)
ステアリングの切り角は、比較的クイックな蛇行運転の操作を想定して1秒間に±10度(±0.17rad)とすると、角速度ωs =2π0.17f=1.10rad/s、角加速度dωs/dt=2π1.10f=6.89rad/s2である。
走行速度を時速100km/h、タイヤ径0.64m とすると ωn=86.81rad/s である。
以上の数値を使ってT3とJmを計算すると次の結果を得る。
切り角によるトルク反力 T3 = 0.10×6.89 = 0.69Nm
ジャイロモーメント Jm = 0.17×86.81×1.10 = 16.2Nm
これだけクイックなステアリング操作を仮定しても、切り角によるトルク反力は無視できるほど小さいことがわかる。Jmはそこそこあるが、パワーステアリングのアシストに埋もれて体感できるか疑問だ。
従って、ホイールの軽量化でステアリングの重さの変化を感じることは、まずないだろう。低速域でステアリングの重さが大きく変化した場合は、空気圧や、タイヤ幅の変動(接地面積の変化)の影響だろう。
ばね下重量の軽減は、ばね上の約10倍の重量軽減に匹敵する!?
販売元、製造元の記事によっては4倍、14倍と記載されているものもあるが、根拠が見あたらない。このような情報によって、
「ばね下を1kg減らしたのだから、車体を10kg以上軽量化したことになる」
と誤解している多いようだ。シャーシやサスペンションにかかる負荷荷重はばね下の質量に比例するから、軽量化は構造の簡素化やコストダウンの為には効果的である。しかしこの理屈からは10倍という数字は出てこない。
10倍という数字はやはり回転慣性に関係した物だろう。そこで、ホイールの回転慣性を、ばね上の質量に換算してみよう。(4-1)式を(4-2)式に代入し、mについて整理すると、
m = 4・ΔI/D2 (6-1)
を得る。これが、回転慣性モーメントの軽量化分ΔIをばね上質量mに変換する式。
表4-1で示した17インチホイールの例を使うと、回転慣性モーメントは、0.0860kgm2 減(4本で0.344kgm2 減)となるから、ΔI=0.344kgm2。タイヤ径D=640mm(乗用車相当)として計算すると、
m = 4×0.344/0.642 = 3.36kg
というように、m (kg)が ΔI (kgm2) に対しほぼ10倍になる。
つまり、慣性モーメントΔIの単位kgm2からm2を省略して読めば「ばね上は約10倍の重量軽減に匹敵する」という謎の説明が作れる。
ところで、この倍率を m/ΔI と置くと式(6-1)は次のように簡単になる。
倍率 = 4/D2 (6-2)
問題の倍率がタイヤ径Dだけで決まる式だ。ここでたとえば、タイヤ径D = 530mm(軽自動車を仮定)とすると約14倍、D = 1m(トラックやバスを仮定)にすると4倍という風に、世間で噂されている様々な係数が求まる。ちなみに、進行方向の慣性は、ばね下を1kg軽量化したら、ばね上でもやはり1kgである。
同じ1キロでも、質量と慣性モーメントは別物。質量を1キロ減らすのはたやすいが、もともと0.2~0.3キロしかない慣性モーメントを1キロ減らすのは不可能。これも結局、商売に都合がよいように、巧妙に作られたセールストークだろう。
路面追従性を良くすると乗り心地は良くなるか
軽量ホイールのメリットについて、次のような説明をみかける。
「ばね下が重いとサスペンションの動きが鈍くなるので乗り心地が悪くなるのです」 (a)
「ばね下が軽くなれば、サスペンションの動きが良くなり、乗り心地や居住性が改善されます」 (b)
これらは一見正しそうに見えるが間違っている。まず、スプリングやばねレートが相対的に上昇することを考慮していない。さらに、路面追従性を良くすると乗り心地は悪い方向に行く。
ホイールが軽くなると路面追従性が良くなるという話は正しい。路面追従性が良くなるということは、ホイールが激しく上下することを意味するし、サスペンションから見れば、路面のおうとつが増えたのと同じこと※5。
※5:グラフ1-1には、タイヤとホイールで決まる16Hzの「共振点」がある。この周波数から下が、ホイールと路面が一体で動く、「つまり100%路面追従する」帯域。
共振点から上は、路面が変動してもホイールが追従して動かない、「路面追従が悪い」帯域である。100%路面追従する帯域では、路面の振動が直接サスペンションのバネに伝わるので、乗り心地が悪くなるのは自明だ。
そもそも「防振」とは路面の上下に追従しないことで発揮される効果。ホイールを軽くするとこの共振周波数が上昇して100%路面追従する条件が拡大する。つまり、ホイールを軽くすればするほど、車体に伝わる振動が増える結果になる。
タイヤが激しく上下動しているのに車体がフラットを保っている図を連想する人もいるだろう。これは、サスペンションのばね定数k2を低くした場合の話であって、ばね下を軽くしてもこの状態を作ることはできない。
従い、(b)は、次のように言い換えると正しくなる。
「サスペンションのばねを弱くすれば、サスペンションの動きが良くなり、乗り心地や居住性が改善されます」 (b’)
「サスペンションの動きが良くなると乗り心地が改善される」のは、摩擦のためにダンパーの動きが悪くなっている不具合を指しているのかもしれない。
結論~軽量ホイールのメリットはあるか
ホイールを軽量化して、慣性を小さくした効果は「加速」に表れるが、上記で仮定したような0-100km/h 10秒の世界では、軽量ホイールのメリットは無いに等しい。
但し、激しい加減速を繰り返す用途、例えばレースの世界では、大きなメリットになる。
もしあなたが軽量ホイールに履き替え、これまでと違う何かを体感できたら、それは軽量化した結果ではなく、空気圧など別の要因によるもの、と考えるのが正しい。
<関連商品>
鋳造ホイール 乗り心地向上に有利な重い鋳造ホイールです
鍛造ホイール レースに好適な軽量ホイールです
自動車技術ハンドブック一覧 この(1)を合わせてご覧ください
<関連記事>
カタログを見ればわかる!~乗り心地の良いクルマの選び方
<改訂履歴>
2015/5/7 グラフの縦軸を振動伝達率から車体に伝わる衝撃に変更。ばね上換算倍率の計算を追補。
補足~もう少しやさしい説明
上記の話をやさしいくまとめてみました。
前提条件
この記事は、タイヤ、サスペンションを変えずに、ホイールだけを軽量化した場合の特性変動について考察したものである。
乗り心地は悪くなる
アルミホイールを軽量化すると、突き上げとロードノイズが増える。揺れに関しては変わらない。揺れはサスのバネによって支配され、ホイールはほとんど関係しないからである。
突き上げとロードノイズ増加に関する具体的な量は、ホイール単体ではなく、ブレーキロータ、キャリパ、ハブ、リンク機構などを含めた、ばね下質量全体の質量をベースとした軽量分の比率で決まる。
例えば、ばね下全体の質量が100kgのとき、ホイールを10kg軽量化したら、乗り心地はおおよそ10%悪化する。
ハンドルの重さは変わらず。高速では直進安定性が悪化
ハンドルの軽さには慣性モーメント(方向軸まわり)とジャイロモーメントの2つが関係する。
慣性モーメントの減少によりハンドルは軽くなるが、変化が小さすぎて体感できない(1Nm以下のきわめて小さいレベル)。
ジャイロモーメントによる影響は低速域ではほとんど体感できず、高速域では直進安定性の悪化要因となる可能性がある。
走りの性能は良くなるが公道ではメリットなし
路面追従性は良くなる。加速性は良くなるが、きわめてわずかである。燃費も良くなるが、数字に出ないごくわずかなレベルである。
加速性向上に関する具体的な量は、車両全体の質量をベースとした軽量化分の比率で決まる。ホイールを10kg軽量化した効果は、トランクの荷物を10kg減らした効果に等しい。
ホイールの回転慣性を軽減した効果は、エンジントルクに対し2桁以上小さいので、全く影響しないとみてよい。
路面追従性に関する具体的な量は、2項同様、ばね下質量全体の質量をベースとした軽量分の比率で改善効果が決まる。
この結論は、「公道レベル」すなわち0-100km/hを10sec程度で加速した場合では、という限定が付く。レースのような加減速の激しい用途では、路面追従性や加速性のメリットが出てくる。
ばね下1キロは、ばね上15キロに匹敵する?
ばね下の1キロは、ばね上でも1キロである。慣性モーメントの1キロなら、ばね上換算で15キロに匹敵するケースがある(慣性モーメントの単位 kgm2 からm2を省略して読む)。従って、この話は次のように言い換えると正しい。
「ばね下の回転慣性質量1キロの軽量化は、バネ上の15キロに匹敵する」
しかしこれは現実的でない。なぜなら、17インチホイールの慣性モーメントは0.3キロ程度で、これを軽量化してもせいぜい0.2キロにしかならず、1キロ低減すること自体が最初から不可能な話だからだ。
路面追従性をよくすると乗り心地が悪くなる
サスペンションからみると、路面追従性がいい、つまりホイールを軽くして動きが良くなればなるほど、ばねの変位が増えて、車体に伝わる力が増える(力=ばね定数×変位)、すわなち、乗り心地が悪化する結果になる。
但し、摩擦による影響でダンパーの動きが悪い場合、つまり、性能の悪いダンパーが使われている場合は、多少動かした方が、等価的なばね定数を下げることができ、乗り心地が向上する可能性がある。
サスペンションやタイヤのバネを柔らかくすることで路面追従性を良くした場合は、乗り心地が良くなる。
違う結果を経験した場合は別のことが原因
ホイールを変えると同時にいろんなものが変わる。最も大きく影響するのが空気圧であり、これが1割変わっただけで、ホイールの影響など吹き飛んでしまう。
ショップでタイヤを脱着すると、空気圧が交換前より高めになる場合がある。すると、ハンドルの重さや加速性、燃費などが体感できるレベルで変化する。
多くの人がこのことを知らないから、軽量ホイールを買った人が、加速が良くなったり、ハンドルが軽くなったのを体感すると、
「これこそが、ホイール軽量化の効果である」
と勘違いしてしまう[1]。
ホイールの影響だけを正確に知るには、タイヤを外す前に空気圧を測っておいて、後で正確に合わせなければならない。ホイールと同時にタイヤを交換してしまった場合は、何の変化を体感しているのか、まったく不明である。
ネット上には数多くのレポートがあるが、こういったことを押さえていない記事は参考にならない。
Q&A
1.計算式は正しいのですか?勝手に作り上げた理屈では?
この検討は、自分で作った独自理論ではありません。使っている運動方程式や数式は教科書に載っているもので、検討の手順も振動の評価として一般的なものです。誰が検討しても同じ結果になります。
2006/2/16補足: 「自動車技術ハンドブック① P265 社団法人 自動車技術会」に当記事とほぼ同じ内容を発見しました。こちらのグラフは模式図で、縦軸は2階微分して加速度になっています。興味のある人はご参照ください。
2.サスペンションのモデル化は正しいのですか
クルマのサスペンションは2質点系モデルで評価するのが一般的です。簡単に書くと次のようになります。
路面の変位->ばね1(タイヤ)->質量1(ホイール)->ばね2->質量2(車体)->車体の変位 (1)
振動伝達率=車体の変位/路面の変位 (2)
ばね1&質量1と、ばね2&質量2で決まる2つの固有値を持ち、それぞれ1桁以上離れているので独立した系と見なす事が可能です。従って(1)式は2分割でき次のようになります。
路面の変位->ばね1(タイヤ)->質量1(ホイール)->ホイールの変位 (3)
ホイールの変位->ばね2->質量2(車体)->車体の変位 (4)
(3)式は高周波、(4)式は低周波の乗り心地に関係するというように、両者の役割分担が異なります。路面の変位は最初にタイヤ&ホイール系で減衰され、残りがサスのばね&車体の系に伝達されて減衰される形になります。
(4)式の「ばね2」への入力は「ホイールの変位」だけが問題であって、「力」や「ホイールの質量」とは無関係な所が注目点です。
車体の変位を乗り心地に近づけて評価するためには、変位を2階微分して加速度に変換する必用がありますが、傾向を知るには車体の変位までを求めて振動伝達率で評価すれば十分です。
実際のものはダンパ、ブッシュ、リンク機構などがありより複雑ですが、モデルを詳細化しても計算精度が上がるだけで基本特性がひっくり返ることはありません※。通常は(3)式のモデルでホイールの変位までを検討すれば十分といえます。
※:摩擦の影響が大きい領域で逆の結果になることがありますが限定された条件にすぎません。
3.自転車やバイクではリムの軽量化は効果ありますが
バイクの場合、車体の質量がクルマと大きく異なるので、上記の結論は当て嵌まりません。運動方程式は同じ物が使えますので、バイクの結果を知りたい場合は、その定数を入れて検討してみるといいでしょう。
4.重いホイールはボディを強く押し上げるから乗り心地は悪くなるのでは?
最もよく聞く間違いの一つです。タイヤやサスペンションの「ばね」の働きが考慮されていません。地面とホイール、ボディを直結して考えています。無論、これでは正しい検討が出来ません。
5.路面にバネ下が追従しないと車体が揺れて乗り心地は悪くなるのでは?
2質点系モデルでは、タイヤ&ホイールと、サスバネ&車重で決まる2つの系を持ち、それぞれ役割分担が異なる点を理解できていません。
車体の揺れ(低周波の路面追従性)はサスバネ&車重で決まる話であって、タイヤ&ホイール決まる路面追従性とは関係ありません。
6.重たい物と軽い物、ぶつかれば重い方が衝撃が大きいはずでは?(2007/3/12追加)
重量の違う物が同じ速度でぶつかるという誤った仮定をしています。
ホイールに加わる力は、ばねのたわみ(変位)に比例しますから、同じおうとつを乗り越えたのなら、ホイールの「速度」ではなくて「加振力」が同じでないといけません。
つまりこのケースは、重たい物と軽い物を「同じ力で加振した」という前提があって、物体もぶつかってくるのではなく「ばね」で受け止める形(変位入力)にしないと間違いです。
重たい物と軽い物、「同じ力で」動かそうとすれば、重たい方が動きが鈍いことは、直感的にも理解できます。
7.タイヤの質量はどのように関係するのですか(2007/3/15追加)
バネ下質量というとタイヤの重さが気になる人も多いようです。通常、ばね要素が質量を持つ場合、1/2ずつをバネの両端に割り振って単純化します。
タイヤの場合、質量の半分以上が路面側に分布すると考えられますので、振動伝達率を評価する場合はタイヤ質量の1/3程度をホイールの質量にプラスすればよいでしょう。
タイヤ質量が数キロ違ってもその1/3しか影響してこないので、これを考慮に入れても大差ないといえます。
8.重たい靴と軽い靴、軽い方が軽快だし加速に有利では?(2007/4/9追加)
クルマの「減速機」が考慮されていません。
ファイナルを含めた総合減速比は通常3~15倍程度ですから、みかけの慣性質量は1/9~1/225となってしまい慣性質量の影響はほぼなくなります。
人間には減速機がありませんので、靴の重さの例えをクルマに当てはめること自体、適当ではありません。
類似の例えに、「同じ重りを背負った場合と、足の先に付けた場合とでは、足の方が重く感じるだろ」というものがあり、これも同様に減速機を無視した不適当な例えです。
<関連商品>
鋳造ホイール 乗り心地向上に有利な重い鋳造ホイールです
鍛造ホイール レースに好適な軽量ホイールです
自動車技術ハンドブック一覧 この(1)を合わせてご覧ください
<関連記事>
1.タイヤ空気圧のマジック~空気圧を変えると走りはこんなに変わる
静かなタイヤの選び方~レグノを超える究極の静音タイヤはこれだ!
スポーツカーにスポーツタイヤは無意味!?~デメリットだらけの高性能タイヤ
R34スカイラインをインチダウンして乗り心地を良くする~キャリパ干渉との戦い
マグネシウム軽量ホイール~RSワタナベ エイトスポークマグ(MAG)を買ってみた